Grado Octavo

PRIMER PERIODO

Actividad para finalizar Primer Período
(Actividad para realizar entre el 20 y el 22 de abril, enviar el 23 de abril)


SEGUNDO PERIODO

Semanas 01 a la 06 (del 04 de mayo al 12 de junio), Lee con atención el tema, mira los ejemplos, da clic sobre algunas palabras y algunos títulos resaltados para acceder a una ampliación de los conocimientos y observa los videos, al terminar ve abajo a la sección de actividades para el grado y realiza la Actividad #1 y #2

Líneas y puntos notables de los Triángulos

Un triángulo, en geometría, es un polígono determinado por tres rectas que se cortan dos a dos en tres puntos (que no se encuentran alineados). Los puntos de intersección de las rectas son los vértices y los segmentos de recta determinados son los lados del triángulo.

Además, dos lados contiguos forman uno de los ángulos interiores del triángulo que, como su propio nombre indica, tiene tres. Y, como es bien sabido, la suma de éstos es 180º.

Entre las rectas (líneas) notables más conocidas de un triángulo son:

1.  Las mediatrices

2.  Las medianas

3.  Las alturas

4.  Las bisectrices

Sus puntos notables asociados son:

1.  El circuncentro

2.  El baricentro

3.  El ortocentro

4.  El incentro

5.  Los exincentros

Clases Magistrales del Docente Apoyo al Primer Taller

Mediatrices y circuncentro

Las mediatrices de un triángulo son las mediatrices de sus lados, es decir, las rectas que pasan por el punto medio de cada uno de sus lados y son perpendiculares a los mismos.

 

La mediatriz de un segmento cualquiera es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de los puntos extremos de dicho segmento. En el caso del lado de un triángulo es, por tanto, el lugar geométrico de los puntos que equidistan de los vértices de dicho lado.

 

Las tres mediatrices del triángulo (hay una por cada lado) se cortan en un punto que está, por tanto, a la misma distancia de los tres vértices del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que pase por los tres vértices. A esa circunferencia se la denomina circunferencia circunscrita, y al centro de la misma en el que se cortan las tres mediatrices circuncentro.

Bisectrices, incentro y exincentros

 

Las bisectrices de un triángulo son las bisectrices de sus ángulos. Existen bisectrices internas (las usuales) y externas a estos ángulos, y son perpendiculares entre sí.

 

La bisectriz de un ángulo es el lugar geométrico de los puntos del plano que equidistan de los dos lados del ángulo.

 

Las tres bisectrices interiores del triángulo (hay una por cada ángulo) se cortan en un punto que está, por tanto, a la misma distancia de los tres lados del triángulo. Eso quiere decir que se puede trazar una circunferencia con centro en dicho punto y que sea tangente a los tres lados del triángulo. A esa circunferencia se la denomina circunferencia inscrita, y al centro de la misma en el que se cortan las tres bisectrices incentro.

 

Además, las bisectrices exteriores de dos ángulos concurren con la bisectriz interior del ángulo restante en puntos denominados exincentros, que son los centros de las circunferencias exinscritas del triángulo. Hay 3 exincentros, al igual que 3 circunferencias exinscritas. Las circunferencias exinscritas son tangentes a un lado y a la extensión de los otros dos.

 

  

Medianas y baricentro

 

Las medianas de un triángulo son las rectas que pasan por uno de sus vértices y por el punto medio del lado opuesto a dicho vértice.

 

Las tres medianas de un triángulo se cortan en un punto llamado baricentro o centroide, G.

 

Se cumple que el baricentro divide a cada mediana con razón 2:1, de manera que la distancia desde el baricentro a cada vértice es el doble que la distancia al punto medio del lado opuesto.

 

Además, cada mediana del triángulo lo divide en dos triángulos de igual área, y las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.

 

También puedes observar otra cosa: uniendo los pies de las medianas (punto medio de cada lado) se obtiene un triángulo semejante al original con área 1/4 del área de éste.

 

En algunos países a las medianas se las llama transversales de gravedad, y esto se debe a que el baricentro coincide con el centro de gravedad del triángulo. Es decir, si cortas un triángulo, por ejemplo, en una cartulina y lo sujetas colgando de un hilo justo en su baricentro, el triángulo se mantiene en equilibrio.

 

Alturas y ortocentro 

Las alturas de un triángulo son las rectas que pasan por uno de sus vértices y son perpendiculares al lado opuesto de dicho vértice, o a su prolongación.

 

Las tres alturas de un triángulo se cortan en un punto llamado ortocentro, H.

 

Características especiales sobre las líneas y puntos notables

Propiedades de las líneas y puntos notables

Clases Magistrales sobre el tema Apoyo al Segundo Taller

Videos de Apoyo sobre el Tema de Líneas notables del triángulo

Semanas 07 a la 09 (del 16 de junio al 02 de julio), Lee con atención el tema, mira los ejemplos, da clic sobre algunas palabras y algunos títulos resaltados para acceder a una ampliación de los conocimientos y observa los videos, al terminar ve abajo a la sección de actividades para el grado y realiza la Actividad #3

Recta de Euler

 

La recta de Euler de un triángulo es una recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo (hay otros puntos notables del triángulo que no hemos visto que también se encuentran en esta recta).

 

Se denomina así en honor al matemático suizo, Leonhard Euler, quien demostró la colinealidad de los mencionados puntos notables de un triángulo, en 1765.

 

Se cumple que la distancia del baricentro al circuncentro es la mitad de la distancia del baricentro al ortocentro. Esta es una de tantas cosas que fascinan de las matemáticas.

  

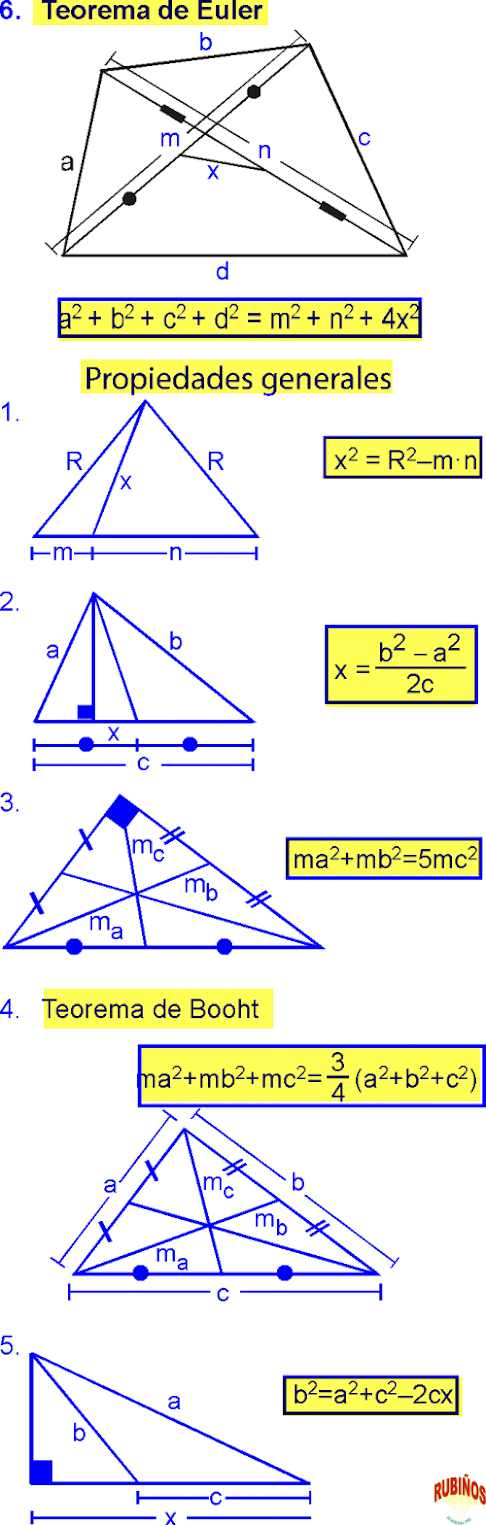
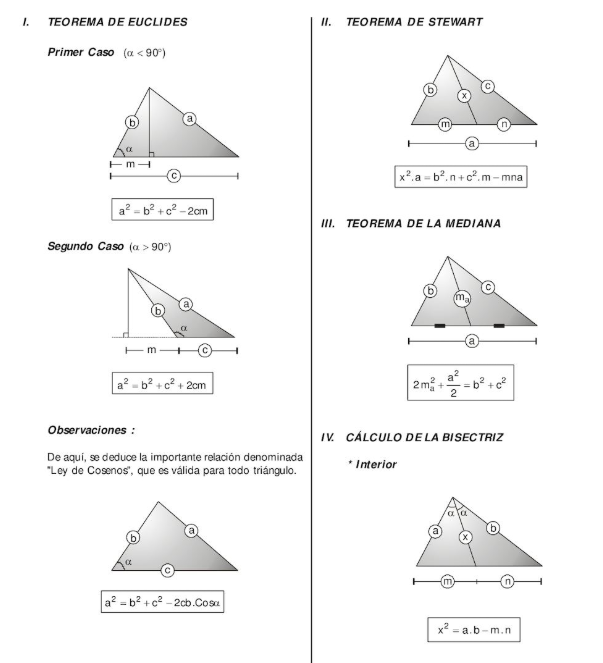
Teorema de la Mediana

En geometría, el teorema de Apolonio, también llamado teorema de la mediana, es un teorema que relaciona la longitud de la mediana de un triángulo con las longitudes de sus lados.

Teorema de Apolonio (teorema de la mediana)

Para todo triángulo la suma de los cuadrados de dos lados cualesquiera, es igual a la mitad del cuadrado del tercer lado más el doble del cuadrado de su mediana correspondiente.

Apolonio de Perga

Para cualquier triángulo ΔABC, si M es la mediana correspondiente al lado C, donde AP = PB = ½C, entonces:

 

Teorema de la Bisectriz 

El teorema de la bisectriz del ángulo interno de un triángulo es un teorema de la geometría elemental la cual es una consecuencia o corolario del Teorema de Tales.

En un triángulo, la razón entre dos lados es igual a la razón de las partes en las que queda dividido el tercer lado por la bisectriz del ángulo interno opuesto.

O lo que es equivalente:

Dado el triángulo ABC, sea AD la bisectriz del ángulo interno A, entonces se cumple la proporción:

En este diagrama, siendo A el ángulo bisecado, BA:AC = BD:DC

Teoremas de las líneas y puntos notables

Clases Magistrales sobre el Tema Apoyo al Tercer Taller

Videos de Apoyo sobre la recta de Euler

Actividades para el Grado Octavo

 

Actividades para realizar, da clic izquierdo sobre cada actividad para descargar el archivo a desarrollar, para cada actividad tendrás un tiempo prudente para realizarla, al finalizar cada actividad debes enviar la evidencia del trabajo terminado en un archivo de Word, (algunas se pueden trabajar directamente en las hojas impresas y luego escanearlas) el archivo debe tener el nombre, el grado, y luego enviarlo todo al correo del profesor dmav1971@gmail.com

 

Actividad #1 Líneas Notables

(Actividad para realizar entre el 4 y el 21 de mayo, envió el 22 de mayo)

 

Actividad #2 Puntos Notables

(Actividad para realizar entre el 26 de mayo y el 11 de junio, envió el 12 de junio)

 

Actividad #3 Teoremas de Euler, Medianas, Bisectriz y otros 

(Actividad para realizar entre el 16 de junio y el 01 de julio, envió el 02 de julio)

Actividades Extras para Niveles Avanzados

 

Estas actividades están diseñadas para las alumnas que son más avanzadas y les gusta desafiar sus conocimientos con más ejercicios para prepararse mejor para sus exámenes.

 

Actividad #1 Líneas Notables para Avanzadas

 

Actividad #2 Puntos Notables para Avanzadas

 

Actividad #3 Teoremas de Euler y otros para Avanzadas

Reto en Casa

Esta es una manera constructiva de ver como lo que se enseña en la materia puede ser aplicable para algo en casa.

Reto para Octavo

En este aparte voy a dejar un reto para que lo hagas en tu casa, debes hacer un video como el mio y enviármelo, con cualquier objeto que tengas a disposición en casa, quien así lo haga tendrá una nota extra que ayudará en el promedio de la materia.