Grado Sexto

PRIMER PERIODO

Actividad para finalizar Primer Período
(Actividad para realizar entre el 20 y el 22 de abril, enviar el 23 de abril)


SEGUNDO PERIODO

Semanas 01 y 02 (del 04 al 15 de mayo), Lee con atención el tema, mira los ejemplos, da clic sobre algunas palabras y algunos títulos resaltados para acceder a una ampliación de los conocimientos y observa los videos, al terminar ve abajo a la sección de actividades para el grado y realiza la Actividad #1

Sistemas de Numeración

Numeración Babilónica

El sistema de numeración mesopotámica (también llamado numeración babilónica) es un sistema de representación de los números en la escritura cuneiforme de varios pueblos de Mesopotamia, entre ellos los sumerios, los acadios y los babilonios.

Aunque su sistema tenía claramente un sistema decimal interno prefirieron utilizar 60 como la segunda unidad más pequeña en vez de 100 como lo hacemos hoy, más apropiadamente se considera un sistema mixto de las bases 10 y 60.

La teoría más comúnmente adoptada es que el 60, un número compuesto de muchos factores (los números anterior y siguiente de la serie serían el 12 y el 120), fue elegido como base debido a su factorización 2×2×3×5, que lo hace divisible por 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, y 30. De hecho, es el entero más pequeño divisible por todos los enteros del 1 al 6.

Numeración Romana

Para la notación moderna de los números romanos se utilizan las siguientes normas: Los números se leen de izquierda a derecha empezando por los símbolos con mayor valor, o conjunto de símbolos de mayor valor.

Un símbolo seguido de otro de igual o inferior valor, suma (por ejemplo X·X·I = 10+10+1 = 21), mientras que si está seguido de otro de mayor valor, ambos símbolos forman un conjunto en el cual debe restarse el valor del primero al valor del siguiente (por ejemplo X·IX = 10+[10-1] = 19).

La unidad (I) y los números con base 10 (X, C y M) pueden repetirse hasta 3 veces consecutivas como sumandos. Los números con base 5 (V, L y D), no pueden repetirse seguidos, ya que la suma de esos dos símbolos tiene representación con alguno de los símbolos anteriores.

La unidad y los símbolos de base 10 también pueden estar restando antes de un símbolo de mayor valor, pero con las siguientes normas: solo pueden aparecer restando sobre los símbolos con base 5 y 10 de valor inmediatamente superiores, pero no de otros con valores más altos (por ejemplo ‘IV’ y ‘IX’, pero no ‘IL’ ni ‘IC’). en el caso de estar restando, no pueden repetirse.

Los símbolos con base 5 no pueden utilizarse para restar (por ejemplo 45 se escribe ‘XLV’ y no ‘VL’).

Videos de apoyo al tema de Números Romanos

Semanas 03 a la 06 (del 18 de mayo al 12 de junio), Lee con atención el tema, mira los ejemplos, da clic sobre algunas palabras y algunos títulos resaltados para acceder a una ampliación de los conocimientos y observa los videos, al terminar ve abajo a la sección de actividades para el grado y realiza la Actividad #2 y #3

Valor absoluto

El valor absoluto de un número entero coincide con su valor numérico sin tener en cuenta el signo. Se representa con unas barras verticales alrededor del número, así: |x|

Por ejemplo,|2| representa el valor absoluto de 2.

Para calcularlo es importante tener apoyo de la representación de los números enteros en la recta numérica.

También es necesario saber calcular el valor opuesto de un número. Es un número que tiene el mismo valor, pero signo contrario. Por ejemplo:

• El valor opuesto de 2 es -2
• El valor opuesto de -2 es 2

Ejemplos

• Cuando es positivo da como resultado el mismo número. Por ejemplo, |5| = 5
• Cuando es negativo da como resultado el número opuesto. Por ejemplo, |-3| = 3
• Cuando es cero,|0| = 0

Como puedes observar, toma siempre un valor mayor o igual que cero.

Además, representa la distancia del número al 0. Ésto es muy fácil de observar en la recta numérica:

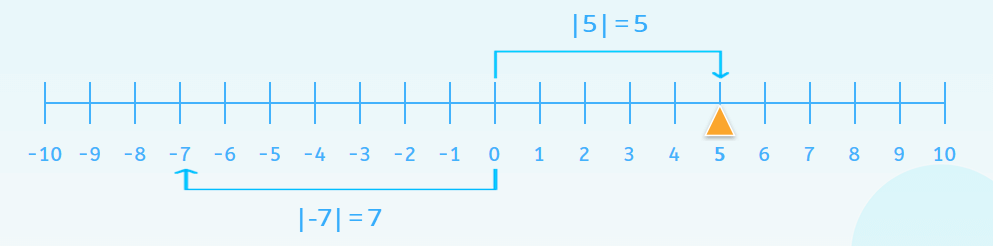
Videos de apoyo a valor relativo y absoluto

Operaciones entre números enteros.

¿Qué son los números enteros?

Los números enteros son el conjunto de todos los números enteros con signo (positivos y negativos) junto con el número 0. Se les representa por la letra Z, letra inicial del vocablo alemán Zahien, también se escribe con la letra z con doble lineado así: ℤ, este conjunto se representa como aparece a continuación:

Z = {…-3, -2, -1, 0, 1, 2, 3, 4…}

Suma y Resta de Enteros.

Para sumar o restar dos números enteros, se determina el signo y el valor absoluto del resultado del siguiente modo:

·         Si dos sumandos tienen el mismo signo: ese es también el signo del resultado, y su valor absoluto es la suma de los valores absolutos de los sumandos.

·         Si dos sumandos tienen distinto signo:

o    El signo del resultado es el signo del sumando con mayor valor absoluto.

o    El valor absoluto del resultado es la diferencia entre el mayor valor absoluto y el menor valor absoluto, de entre los dos sumandos.

·         La resta de dos números enteros (minuendo menos sustraendo) se realiza sumando el minuendo más el sustraendo cambiado de signo.

Ejemplos Suma.

(+21) + (−13) = +8

(+17) + (+26) = +43

(−41) + (+19) = −22

(−33) + (−28) = −61

Ejemplos Resta.

(+10) − (−5) = (+10) + (+5) = +15

(−7) − (+6) = (−7) + (−6) = −13

(−4) − (−8) = (−4) + (+8) = + 4

(+2) − (+9) = (+2) + (−9) = −7

Semanas 07 a la 10 (del 16 de junio al 10 de julio), Lee con atención el tema, mira los ejemplos, da clic sobre algunas palabras y algunos títulos resaltados para acceder a una ampliación de los conocimientos y observa los videos, al terminar ve abajo a la sección de actividades para el grado y realiza la Actividad #4 y #5

Multiplicación y División.

En la multiplicación y en la división de dos números enteros se determinan el valor absoluto y el signo del resultado de la siguiente manera:

·         El valor absoluto es el producto (o cociente) de los valores absolutos de los factores (o del dividendo y divisor).

·         El signo es "+" si los signos de los factores (o del dividendo y divisor) son iguales, y "−" si son distintos.

Regla de los signos - Multiplicación y División

·         (+) × (+) = (+) Más por más igual a más.

·         (+) × (−) = (−) Más por menos igual a menos.

·         (−) × (+) = (−) Menos por más igual a menos.

·         (−) × (−) = (+) Menos por menos igual a más.

Ejemplos multiplicación.

(+5) × (+3) = +15

(+4) × (-6) = -24

(−7) × (+8) = −56

(−9) × (−2) = +18

Ejemplos división.

(−16) ÷ (+4) = −4

(−18) ÷ (−2) = +9

(+15) ÷ (+3) = +5

(+12) ÷ (-6) = -2

Videos de Apoyo a las Operaciones con enteros

Actividades para el Grado Sexto

 

Actividades para realizar, da clic izquierdo sobre cada actividad para descargar el archivo a desarrollar, para cada actividad tendrás un tiempo prudente para realizarla, al finalizar cada actividad debes enviar la evidencia del trabajo terminado en un archivo de Word, (algunas se pueden trabajar directamente en las hojas impresas y luego escanearlas) el archivo debe tener el nombre, el grado, y luego enviarlo todo al correo del profesor dmav1971@gmail.com

Actividad #1 Números romanos
(Actividad para realizar entre el 4 y el 14 de mayo, envió el 15 de mayo)

Actividad #2 Suma de enteros

(Actividad para realizar entre el 18 y el 28 de mayo, envió el 29 de mayo)

Actividad #3 Resta de enteros

(Actividad para realizar entre el 01 y el 11 de junio, envió el 12 de junio)

Actividad #4 Multiplicación de enteros

(Actividad para realizar entre el 16 y el 25 de junio, envió el 26 de junio)

Actividad #5 División de enteros

(Actividad para realizar entre el 30 de junio y el 09 de julio, envió el 10 de julio)

Actividades Extras para Niveles Avanzados

Estas actividades están diseñadas para las alumnas que son más avanzadas y les gusta desafiar sus conocimientos con más ejercicios para prepararse mejor para sus exámenes, por lo tanto no tienen una valoración o una nota para el período.

Actividad #1 Números romanos para Avanzadas

Actividad #2 Suma de enteros para Avanzadas

Actividad #3 Resta de enteros para Avanzadas

Actividad #4 Multiplicación de enteros para Avanzadas

Actividad #5 División de enteros para Avanzadas

Reto en Casa

Esta es una manera constructiva de ver como lo que se enseña en la materia puede ser aplicable para algo en casa.

Reto para Sexto

En este aparte voy a dejar un reto para que lo hagas en tu casa, debes hacer un video como el mio y enviármelo, con cualquier objeto que tengas a disposición en casa, quien así lo haga tendrá una nota extra que ayudará en el promedio de la materia.